10.19
T1异或:
题意:c_i = a_i\ xor\ b_i, 求 c 的最小字典序。
对 a,b 建立 01 trie, 每次将可能成为最小数的值加入c, 最后排序。
T2仓皇逃跑:
题意:一棵树每条边有k种颜色有m条路径是有两种以上的颜色,求染色方案。
容斥,考虑包含集合 s 的边,并钦定被包含的边形成的连通块染同一种颜色,染色方案即为cnt^k。
T3有根树:
题意:有两棵树我们认为边 (u,v) 有害于另一条边 (x,y) ,仅当最开始时1.不属于同一棵树 2. (u,v) 中只有一个点属于 (x,y) 的子树。现在删了第一棵树的边 (x, y), 每次删除有害于当前边的边,并把删除的边作为下次操作的集合。直到不能操作。
形式化条件:
dfn_x <= dfn_u <= dfn_y 且 dfn_x > dfn_v\ or\ dfn_y
放在二维平面上可发现一定是一段前缀和后缀,对于u,v分别维护然后标记每一条边是否删过。
T4膜拜:
10.21
T1不连续子序列:
题意:有0,1,2,3的序列将0替换为1,2,3后使得最多出现次数的元素>\frac{n}{2}的方案。
分讨,对于n=4暴力
T2造题:
题意:小X可以选择一条左下到右上的路径并将上面的权值变为0,小Y可以选择左上到右下的路径。小X想让小Y得分最小,小Y想最大化的分,求最终得分。
令 dp_{i,j,k,0/1} 为当前到 (x,y) 且最后一段长为 k 是从上面还是右边转移过来。
T3机器人:
简单题跳过
T4岛屿:
题意有一个大连通块岛屿有若干个火山还有海,求一条路径完全包括岛屿且包含(x_i,y_i)并离火山距离最大。对于每个询问求出最大距离。
考虑从岛屿任意一点引出一条直线一条合法路径必然穿过这条线奇数次。然后定义两个点 dis(x,y,0/1) 表示 (x,y) 这个点穿过线奇数还是偶数次且与火山最远距离。连边就是向四联通点连边如果跨过了线就0->1。最后在 krusal 重构树上的 lca((x_i,y_i,0),(x_i,y_i,1))的权值就是答案。
10.22
T1生成树1:
题意:判断k颗树是否满足任意两条路径除端点外无交。
结论一个点只能在至多一棵树上不为叶子
T2生成树1
题意:tpye = 1 构造 \frac{n}{2} 颗树满足任意两条路径除端点外无交。
tpye = 0 构造 \frac{n}{2} 颗树不满足任意两条路径除端点外无交。
type = 1 分为 \frac{n}{2} 组每组中的两个点不做叶子其他做叶子。
type = 0 在上一个的基础上将两个非叶子节点的叶子中最小和次小连边并断开最小点和非叶子节点的边
T3互质询问:
题意:操作1:加入一个数。操作2:询问权值l – r之间是否都互质。
用 set 维护每个质数的出现位置。在线段树上维护每个数和它 gcd 不为1的数的最小的位置。
T4数字串:
题意:一个字符串,把它分割为若干段,在满足单调递增且最大值最小的情况下字典序最大。
f_i 为结尾位置为i的最大的上一个串的结尾位置。显然 (f_i,i) 可以更新的区间是有决策单调性的最后 f_n 就是最小值
然后令 g_{f_n}=1 如果有前导0则把前导0全赋为1。倒着 dp 一遍。更新要用线段树。判断两串大小用二分哈希。
10.24
T1垃圾桶:
模板题
T2联通块:
题意:一张 2 * n 的图,有黑白两种颜色,一个连通块中选黑色会加1,选白色会减1。小 A 可以
交换上下两行且这个操作最多 m 次,小 A 想让权值最小,小 B 想让权值最大。求最终答案。
显然对于黑白一列只选一个黑色那一定满足个数 >2m, 否则就黑白都选。
第一种 dp, 第二种最大子段和。
T3序列:
给定一个长度为 n 的非负整数序列 a,初始时所有数均被标记为蓝色,youyou 和 yy 轮流对序列 a 进行操作,由 youyou 开始。
- 如果当前是 youyou 的回合,那么他可以选择一个长度至多为 c_1 的区间,如果该区间内所有数的和小于等于 w_1,则标记该区间所有数为红色。
-
如果当前是 yy 的回合,那么他可以选择一个长度至多为 c_2 的区间,如果该区间内所有数的和大于 w_2,则标记该区间所有数为蓝色。
如果当前操作方没有可操作的区间,他将跳过本回合。
定义 youyou 胜利即是在游戏任意时刻,所有数都被标记为红色。定义 yy 胜利则是在 10^{51971} 个回合内,youyou 无法胜利。两者都会以最优策略进行游戏。
但是他们认为这个游戏太简单了,于是决定上上强度。
现在给定 q 个操作,对于每个操作给定三个数 opt,x,y。
- 如果 opt 为 1,表示将 a_x 增加 y(0\le y \le 10^9)。
- 如果 opt 为 2,表示 youyou 和 yy 将在区间 [x,y] 所形成的序列上进行一轮游戏。
对于每个 opt=2 的操作,请你求出在区间 [x,y] 所形成的序列上进行游戏,youyou 能否获得胜利。如果 youyou 能胜利,输出 cont;否则,输出 tetris。
将一个点改为以它为结尾的一段区间的和,单点修改改为区间修改。用线段树二分找第一个满足和最后一个满足的位置。分讨一下即可。
T4三进制数:
现在有 0 \sim n 共 n + 1 个数。
定义 (x)_ {3} 表示十进制数 x 的三进制形式。如果没有特别强调,那么这些数均为十进制形式。
youyou 想构造一个序列长度为 p(p \ge 1)的非负整数序列 a。使之满足:
a_i \in [0,n]。
不存在 i,j(1 \le i <j \le p),使得 a_i = a_j。
对于任意 1 \le i
1.(a_i)_ 3 去掉最后一位,恰好等于 (a_{i+1})_ 3(若只有一位,则去掉后的数字为 0)。
2.在 (a_i)_ 3 末尾添上某一位 t(0 \le t \le 2),恰好等于 (a_{i+1})_3(若 a_i = 0,则添加后舍去前置 0)。
3.a_i \le w, (a_i)_ 3 的末尾不是 0,且将末尾的一位数字移到开头与 (a_{i + 1})_3 相等。
4.当 (a_i)_ 3 长度 \ge 2,且 (a_i)_ 3 次高位非零时,将 (a_i)_ 3 开头的一位数字移到末尾,形成的数的十进制值 \le w,且恰好等于 (a_{i+1})_ 3。
这样的序列 a 被称为“完美的”。
youyou 认为,如果十进制三元组 (x,y,z) 是好的,必须满足以下条件:
0 \le x,y,z \le n,x \neq y。
存在至少一个”完美的“序列 b,使得十进制下有 b_1=x,b_s = y。其中 s 为序列长度。
存在至少一个”完美的”序列 c,使得十进制下有 c_1=z。同时,对于上述任意的 b,均有恰好一对 (i, j),满足 1 \le i \le |b|,1 \le j \le |c|,使得 b_i = c_j。
对于每一个 0 \le z \le n,求能构成“好的”三元组 (x,y,z) 的有序对 (x,y) 的个数。
先对合法数字连边,然后在图上观察,合法路径其实就是一个点 z 满足到 x, y 之间的所有路径经过的第一个点是是同一个点,因为如果有两个点的话必然会形成一条经过 z 的新路径
这很圆方树,于是在圆方树的圆点上考虑以这个点作为交点的方案。
10.28
T1照相:模拟
T2子序列:
题意:有一个序列只含 A, B,C 有 AB, AC, BC 三种匹配方法,求一组构造使原串分成 n/2组并输出方案。
先检查C是否能怕匹配完,再从后往前匹配 B
T3厨师:

按 b_i 排序,观察发现 k 的答案可以由 k – 1 的答案加上一个数得到。
就可以dp。然后有凸包优化但不会。
T4:???
10.29
T1最大公约数:从大到小容斥
T2删除:
构建一个双射,就是对一个最终局面,考虑其中的点如果能删左下就删左下,能删右上就删右上。就有一个dp f_{i,j,k} 表示当前处理到第 i 列,上
一个删左下的是 j,上一一个删右下的是 j,转移有四种分别是 f_{i, j, k}->f_{i+1, j, k}\ f_{i + 1, i + 1, k}\ f_{i + 1, j, i + 1}\ f_{i + 1, i + 1, i + 1} 为了方便计数可以加入 0,和n + 1 号点,转移的条件首先是两点之间的矩形没有其他点,然后是两点列的关系是否合法。
T3树:
题意:一颗树,求两条不交路径,使其异或值之和最大。
考虑用01 trie 把全局最大链提取出来吗,答案要么包含它,要么包含它的一部分。
首先包含它就可以把它的子树再求一遍最大链。
包含它的一部分就是将其中一条边断开,对于两颗子树求最值。这可以前后缀 max处理
T4平方:

可以先把每个数表示为原根形式,然后根号分治即可,简而言之就是对于x_i中的点如果出现次数 \le \sqrt n 就在 x_i处改,否则就加 tag,最后在 y_i 乘tag。
求离散对数可以先预处理出前 B 个中的质数,在欧拉筛求出前求离散对数可以先 BSGS 出前 B 个中的质数,在欧拉筛求出前 B 个。现在有公式
p \equiv ux + v
Case1: x \equiv \frac{P – v}{u} => log(x) \equiv log(-1) + log(v) – log(u)
Case2: x \equiv \frac{P + x – v}{u} => log(x) \equiv log(x – v) – log(u + 1)
显然每次递归是 min(v, x – v) 这显然每次至少除二。
10.31
T1记忆之桥:给出两点最短路奇偶性,求构造连边方案。
先对奇数点对连边,跑floyd 检查和原图是否一样。
T2作业规划:简单dp
T3殊途同归:给定两棵树给出 a, b 求一个点 x 是它在两颗树中与 a, b
的距离和最远。
一个点到直径两端点距离最远。可以用线段树维护一段区间的点在第二棵树上的直径(类似与虚树直径,这要加上当前点在树一中的距离)。合并直接二条直径端点两两组合求最值即可。
T4单调递增:首先第二种移动方式显然不包含。于是套路建树。设f_u为从u到rt的最小代价,g_u 为从最左点走出 u 的子树的最小代价,sum_u为从
从最左边的兄弟到u的 g的值之和,相当于从从最左边到u的最小花费,还要加上sum_{fa}。
auto query = [&] (int x, int y) {
int l = lca(x, y);
if (l == y) return f[x] - f[y];
int fx = kth(x, dep[x] - dep[l] - 1);
return f[x] - f[fx] + sum[y] - sum[fx] - g[fx] + a[fx] + g[y] - a[y];
};
11.2
T1数字串:简单题
T2简单题:区间不同颜色升级版
T3西西弗西: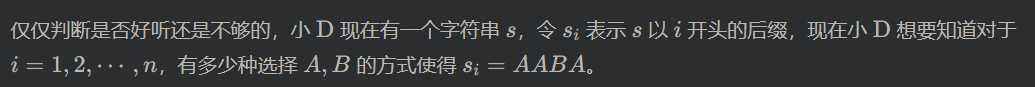
将后缀排序可以发现一个后缀A的贡献区间是一个连续段。
T4:???
11.4
T1随机:枚举 mex
T2像素之旅:构造
T3数据删除:

先容斥一下,发现最难的条件是求独立集个数。设 S 表示还剩那些点没考虑。
然后取其中最小点考虑将它是否在独立集中,在就是将它和它相邻的点删除,不在
就直接删除。复杂度T(n)=T(n-1)+T(n-2)记忆化一下可过。
T4高分值:
首先当前点的答案一定是在前一个点最优答案的基础上改。
维护最优答案的结尾。对于奇数显然是删除大于的,然后将剩下的翻转。
对于偶数先检查 \frac{a_i}{2} 是否在其中,如果在最优答案就只剩 \frac{a_i}{2} 否则就加入 \frac{a_i}{2} 然有在翻转。观察发现最优答案一定形如一段区间和若干散点,可以用set 和 kx+b形式维护散点。
11.5
T1排列:构造
T2可重集:一个可重集S={a_i+b_j+c_k}求第k大
伪算不好卡但还是贴一个正解

T3传说:
先建出最短路径树然后设g_u为将u-fa这条边删掉从u出发的答案,显然有g_u=min(g_u,dis_x+dis_y+w_{x,y}-dis_u),答案就是 f_u = max(g_u, f_v + dist(u, v))用类dijkstra跑就行了。
T4染色:决策单调性。
11.7
对于 tp=1,显然有dp_i = (\Sigma\ dp_j * (i – j)) + 1,发现 i-j 都是 p 的倍数,那就相当于每次 dp_j 系数加上 p。就可以矩阵优化转移。
对于 tp=2,就是在 tp=1 的基础上把加一改为加 i并前后都 dp 一遍。
就是相当于把环从一处断开。
T3:决策单调性
T4:巨大困难题
11.9
T1树:结论 or 观察题
T2宠物狗:集合hash + 字符串 hash
T3:???
T4:???
